مهندسی معکوس مدل های سه بعدی
بررسی منطق نرم افزارها و ابزارهای ارائه شده در حوزه
معکوس (طراحی)
یکی از رویکردهای متداول برای جستجوی گزینه های طراحی ، تغییر اندازه یا شکل سیستم مکانیکی است ( طراحی 3D ).
برای تغییر اندازه یا شکل قطعه، قطعات و مونتاژ باید به اندازه کافی پارامتریک شوند تا اهداف طراحی بدست آید.
در سطح قطعات ، پارامترسازی طراحی به معنای ایجاد ویژگی های سالید و ابعاد مربوطه است
به طوری که هنگام تغییر مقدار ابعاد می توان قطعه را به درستی بازسازی کرد
و قسمت بازسازی شده اهداف طراحی را نشان می دهد.
در سطح مونتاژ ، پارامتر سازی طراحی شامل تعریف مجموعه قطعات مونتاژ و ابعاد مربوط به قطعات است.
هنگامی که یک مونتاژ کاملاً پارامتریک شده باشد،
تغییر در اندازه ابعاد می تواند به طور خودکار به تمام قطعات تحت تاثیر انتشار یابد.
قطعات تحت تاثیر باید با موفقیت بازسازی شوند و در عین حال باید موقعیت و جهت گیری مناسب را
بدون نقض هرگونه قید مونتاژی، ایجاد تداخل قطعات
و یا ایجاد فاصله ی بیش از حد نسبت به یکدیگر حفظ کنند.
به عنوان مثال، در یک موتور تک پیستونی که در شکل 1 نشان داده شده است.
تغییر قطر سوراخ بدنه موتور نه تنها هندسه بدنه را تغییر خواهد داد،
بلکه کلیه قسمت های دیگر را نیز تحت تأثیر قرار می دهد،
مانند پیستون ، آستین پیستون و حتی میل لنگ.
علاوه بر این ، همه آنها باید به درستی بازسازی شوند
و کل قیدهای مونتاژ باید حفظ شود و اهداف طراحی را به درستی نشان دهد.
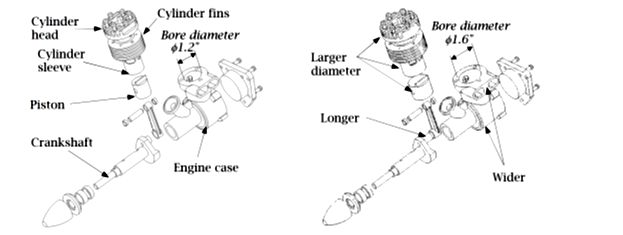
شکل1- نمای انفجاری موتور تک پیستون a) قطر سوراخ 1.2 اینچ b) قطر سوراخ 1.6 اینچ
1- مهندسی شکل
روند کلی مهندسی شکل و مدل سازی سالید پارامتریک در شکل 2 نشان داده شده است
که در آن چهار مرحله اصلی درگیر هستند.
فاز (1) مثلث سازی هست که در آن ابرنقاط را به مش چند ضلعی تبدیل می کنند ،
فاز (2) تقسیم مش که مش چند ضلعی را بر اساس مشخصات هندسه سطحی قطعه ،
تبدیل به مناطق جدا از هم می کند ،
فاز (3) مدل سازی سالید که مناطق تقسیم شده را به مدل های جامد پارامتریک تبدیل می کند،
و فاز(4) تبدیل مدل که مدل های سالید ساخته شده را
به صورت سازگار با سیستم های CAD اکسپورت می کند.
توجه داشته باشید که مطلوب است که کل فرآیند کاملاً خودکار باشد.
بجز فاز 3. این بدان دلیل است که فاز 3 عمدتا برای بازیابی اهداف اصلی به تعامل طراح نیاز دارد.
این چهار مرحله به طور خلاصه در ادامه بحث شده است.
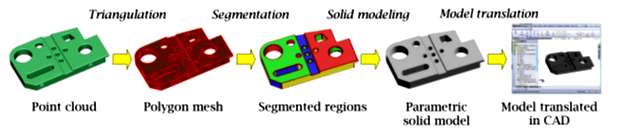
شکل2- روند کلی مهندسی شکل و ساخت مدل سالید پارامتریک
1-1 -مثلث بندی
تئوری ریاضی و الگوریتم های محاسباتی مثلث سازی در چند دهه گذشته به خوبی توسعه یافته است.
یک شبکه چند ضلعی را می توان به طور خودکار
و کارآمد برای مجموعه داده شده از نقاط داده ایجاد کرد.
مفهوم اساسی در مثلث سازی، مثلث بندی Delaunay است.
علاوه بر مثلث سازی Delaunay ، چندین الگوریتم ریاضی مشهور برای مثلث سازی وجود دارد،
از جمله marching cubes، alpha shapes، الگوریتم چرخش توپ یا ball pivoting algorithm (BPA)،
بازسازی سطح پواسون، moving least squares و غیره.
چند پروژه امجام شده در این حوزه نتایج قابل توجهی ارائه داده اند،
مانند بخشهایی از Florentine Pietà اثر میکل آنژ
که متشکل از 14 میلیون شبکه مثلثی که از بیش از 700 اسکن ایجاد شده است،
بازسازی “کلیسای جامع پیزا” (پیزا ، ایتالیا) از اسکن های لیزری با بیش از 154 میلیون نمونه،
و ساختارهای سر و مغز (مخفی) از 150 قطعه MRI استخراج شده
با استفاده از الگوریتم marching cubes (حدود 150،000 مثلث)،
همانطور که در شکل 3 نشان داده شده است.

شکل3- پروژه های نمونه اسکن و مثلث سازی (الف) Florentine Pietà ، (ب) کلیسای جامع پیزا و (ج) ساختارهای سر و مغز.
1-2-بخش بندی
یکی از مهمترین مراحل مهندسی شکل ، تقسیم بندی مش است.
تقسیم بندی نقاط اصلی داده یا مش را به زیرمجموعه هایی تقسیم می کند
که منطقاً هر یک از آنها متعلق به یک سطح اولیه هستند.
به طور کلی، تقسیم بندی فرآیندی پیچیده است. غالباً از تکنیک های رشد منطقه تکرار شونده استفاده می شود.
بعضی از آنها از روشهای غیر تکراری به نام تقسیم بندی مستقیم استفاده می کنند که کارآیی بیشتری دارند.
به طور کلی فرآیند تقسیم بندی شامل یک الگوریتم سریع
برای جستجوی k-nearest neighbors و برآورد خصوصیات سطح مرتبه اول و دوم است.
تقسیم بندی مرتبه اول که بر اساس بردارهای عادی است ،
یک تقسیم اولیه از سطح را فراهم می کند و لبه های تیز و
همچنین نواحی صاف یا بسیار خمیده را تشخیص می دهد.
تقسیم بندی مرتبه دوم با توجه به انحناهای اصلی، سطح را تقسیم می کند
و مبنای مناسبی برای طبقه بندی سطوح جبری ساده را فراهم می کند.
نتیجه ی تقسیم بندی مش، تابع چندین پارامتر مهم است،
مانند مقدار k (تعداد نقاط همسایه که برای تخمین خصوصیات سطح انتخاب شده اند)،
و اختلافات تعیین شده در بردارهای نرمال و انحناها
(که به آنها آستانه حساسیت نیز گفته می شود) که نقاط داده یا مش را گروه بندی می کند.
به عنوان مثالی که در شکل 4 (الف) نشان داده شده است ،
یک آستانه با حساسیت بالا، منجر به مناطق پراکنده
در اندازه های کوچک می شود و یک آستانه با حساسیت پایین تر
تمایل به ایجاد مناطق تقسیم شده ای دارد که شباهت زیادی به توپولوژی جسم دارند،
همانطور که در شکل 4 (ب)نشان داده شده است.

شکل4- مثالی از تقسیم بندی مش. (الف) جسمی که به دلیل آستانه حساسیت زیاد در بسیاری از مناطق کوچک تقسیم شده است و (ب) مناطقی که با آستانه حساسیت کم تعیین می شوند.
بیشتر الگوریتم های تقسیم بندی، انطباقی را ارائه می دهند
که در آن منطبق ترین نوع از سطوح پایه برای هر ناحیه از تقسیم بندی اختصاص می یابد.
تعیین سلسله مراتب انواع سطح به ترتیب پیچیدگی هندسی ، مهم است (مانند شکل 5).
به طور کلی، اشیا توسط سطوح اولیه (یا عملکردی) نسبتاً بزرگ محدود می شوند.
سطوح اولیه ممکن است در امتداد لبه های تیز به یکدیگر برسند
یا ممکن است سطوح ثانویه یا ترکیبی وجود داشته باشد.

شکل5- سلسله مراتب سطوح
همانطور که در بالا بحث شد، تقسیم بندی مبتنی بر ویژگی
مبنای مناسبی برای طبقه بندی سطوح جبری ساده را فراهم می کند.
سطوح جبری ، مانند صفحه ها ، چهارگوشه های طبیعی (مانند کره ، استوانه ها و مخروط ها)،
به راحتی در چنین مناطقی قرار می گیرند.
روشهای مختلفی برای ساپورت چنین انطباقاتی ، با استفاده از moving least squares ارائه شده است.
علاوه بر سطوح جبری ابتدایی ، سطوح عمومی تر با یک تولید حرکت ساده (simple kinematic generation)،
مانند سطوح sweep ، سطوح چرخان (sweep چرخش)، سطوح اکستروژن (sweep انتقال)
و سطوح لوله ای به طور مستقیم با مدل های CAD سازگار هستند.
متناسب کردن این سطوح با نقاط داده یا مش تقسیم بندی شده،
برای بازسازی مدل های سطح و پشتیبانی از پارامترسازی بسیار مهم است.
در برخی موارد، همه مناطق تقسیم شده نمی توانند با رعایت حاشیه خطای مجاز،
منطبق بر سطوح اولیه یا سطوح سازگار با CAD باشند.
این مناطق باقیمانده به عنوان سطوح Free Form طبقه بندی می شوند،
جایی که هیچ نظم هندسی یا توپولوژیکی قابل تشخیص نیست.
اینها می توانند مجموعه ای از تکه های به هم چسبیده (Patches)
و یا تکه های اصلاح شده باشند. آنها اغلب با سطح NURBS منطبق می شوند.
الگوریتم ها و روش های بسیاری برای پشتیبانی از انطباق سطح NURBS ارائه شده است.
1-3-مدل سازی سالید
مدل سازی سالید احتمالاً کمترین پیشرفت را در روند کلی مهندسی شکل دارد.
روشهایی برای ساخت خودکار مدلهای B-rep از ابر نقاط یا مش مثلثی وجود دارد.
برخی از آنها برای شناسایی ویژگی های تولید برای برنامه ریزی فرایند متمرکز بودند.
یکی از پیشرفت های امیدوار کننده در سال های اخیر، شناسایی ویژگی های هندسی (GFR) است
که به طور خودکار ویژگی های سالید تعبیه شده در مدل های B-rep را تشخیص می دهد.
با این حال، هیچ یک از این روش ها نمی توانند فرآیند ساخت را به طور کامل خودکار کنند
و مدل های سالید کاملاً پارامتریک تولید کنند.
انتظار می رود مقداری از کار به طور دستی صورت گیرد.
BoundaryRepresentation1-3-1
بر اساس مناطق تقسیم شده (با سطوح انطباقی)، یک نمودار مجاور منطقه ساخته می شود
که توپولوژی کامل را منعکس می کند و به عنوان پایه ای
برای ساخت مدل نهایی B-rep که به آن ها مدل های دوخته شده نیز اطلاق می شود،
عمل می کند؛ که در آن سطوح بدست آمده در امتداد لبه های مشترکشان به هم چسبانده می شوند.
به طور کلی ، در ساخت مدل های B-rep سه مرحله وجود دارد ، مسطح سازی (flattening) ،
محاسبات لبه ها و رئوس (edges and vertices calculations) و دوخت (stitching).
در مرحله flattening ، مناطق تا بیرون امتداد می یابند تا همه مثلث ها طبقه بندی شوند.
توجه داشته باشید که این مرحله برای از بین بردن تمام شکاف ها و گپ های بین مناطق لازم است.
لبه های تیز را می توان با استفاده از روال تقاطع سطح-سطح محاسبه کرد
و راس هایی که سه سطح با هم روبرو می شوند نیز تعیین می شود.
در طی فرآیند ، یک درخت توپولوژی کامل B-rep نیز ساخته می شود.
سپس با دوخت وجوه، لبه ها و رئوس، مدل B-rep ایجاد می شود.
این عملیات معمولاً توسط اکثر کرنل های مدل سازی سالید پشتیبانی می شود.
1-3-2-شناسایی ویژگی های هندسی
مدل های B-rep مبتنی بر ویژگی نیستند.
برای تبدیل یک مدل B-rep به یک مدل سالید مبتنی بر ویژگی،
ویژگی های سالید تعبیه شده باید شناسایی شوند و یک درخت ویژگی که توالی ایجاد ویژگی را توصیف می کند،
ایجاد شود. یکی از موفق ترین الگوریتم های تشخیص ویژگی هندسی توسط Venkataraman پیشنهاد شده است.
الگوریتم با استفاده از یک فرایند ساده چهار مرحله ای ،
(1) ساده کردن وجه های وارد شده،
(2) تجزیه و تحلیل وجه ها برای هندسه ویژگی خاص،
(3) حذف ویژگی شناخته شده و به روز رسانی مدل.
(4) بازگشت به مرحله 2 تا زمانی که همه ویژگی ها شناخته شوند.
این فرآیند در شکل 6 نشان داده شده است.
پس از شناسایی تمام ویژگی های ممکن،
آنها روی یک مدل سالید جدید از قطعه ایجاد می شوند (شکل 6 (d).)؛
که به صورت پارامتریک با یک درخت ویژگی که بازتولید ویژگی (یا بازسازی مدل)
را با رعایت توالی تعریف می کند، همراه خواهد بود.

(الف) مدل سطح واردشده با سطح سوراخ انتخاب شده ،
(ب) سوراخ شناسایی شده و برداشته شده، وجه اکسترود شده ی سیلندر انتخاب شده،
(ج) اکستروژن استوانه ای شناسایی شده، وجه اکستروژن بلوک پایه انتخاب شده و
(د) همه ویژگی ها شناسایی شده و در مدل سالید ایجاد شده اند.
روش Venkataraman ابتدا توسط Geometric Software Solutions, Ltd. (GSSL) تجاری شد و
در تعدادی از بسته های CAD، از جمله SolidWorks و CATIA پیاده سازی گردید
که قابلیت شناسایی ویژگی های اساسی مانند اکسترود، چرخش و اخیراً Sweep را دارا می باشد.
این قابلیت در درجه اول برای پشتیبانی از انتقال مدل های سالید
بین بسته های CAD با موفقیت حاصل شده است،
که در آن نه تنها ویژگی های هندسی (که توسط IGES انجام شده است)
بلکه ویژگی های پارامتریک نیز منتقل می شوند.
یکی از مهمترین مواردی که در نرم افزار تجاری GFR آشکار شده است ، بازیابی قصد طراحی است.
به عنوان مثال ، فلنج لوله هواپیما به عنوان یک ویژگی چرخشی منفرد شناخته می شود،
جایی که یک اسکتچ حول یک محور می چرخد (شکل 7 (a)).
با این حال، پیاده سازی های فعلی GFR انعطاف پذیر نیستند.
همانطور که در شکل 7 (ب) نشان داده شده است ، بدون تعامل کافی کاربر،
فلنج تک اسکتچه، ممکن است به عنوان چهار یا چند ویژگی جداگانه شناخته شود.
در حالی که قطعات سالید نهایی از نظر فیزیکی یکسان هستند، اما پارامترهای تعیین کننده آنها یکسان نیستند.
این پیاده سازی به حالت دسته ای ممکن است در بازیابی اهداف معنی دار طراحی مورد نظر نباشد.

(الف) ویژگی تک چرخش (single revolved)، و
(ب) چهار ویژگی: چرخش ، اکسترود ، برش و فیلت.
1-3-3-پارامتریک سازی طراحی
یک مدل سالید پارامتریک مبتنی بر ویژگی از دو عنصر اصلی تشکیل شده است:
یک درخت ویژگی و اسکتچ هایی کاملاً پارامترسازی شده.
یک اسکتچ کاملاً پارامتریک شده به این معنی است که مشخصات اسکتچ کاملاً مقید و دارای ابعاد است،
بنابراین تغییر در مقدار ابعاد، بازسازی را همانطور که با اهداف طراحی پیش بینی شده، به همراه دارد.
تا کنون هیچ روش پیشنهادی یا ارائه شده ای وجود ندارد که فرآیند را کاملاً خودکار کند.
برخی از قابلیت ها توسط ابزارهای تجاری، مانند Rapidform و GeoMagic ارائه شده اند
که از طراحان برای ایجاد اسکتچ های کاملاً پارامتریک شده به صورت تعاملی پشتیبانی می کنند،
که به طور دقیق با نقاط داده مطابقت دارند و تلاش برای مدل سازی را بسیار تسهیل می کنند.





دیدگاهتان را بنویسید
می خواهید در گفت و گو شرکت کنید؟خیالتان راحت باشد :)